随机数生成器
我自己的课程作业，感觉写得还行，放到这里来，免得丢掉了。
| 摘要: | 本文对随机数生成器的不同使用环境及要求、类别及检验方法进行综述。 |
|---|---|
| 关键词: | 随机数生成,RNG，PRNG，TRNG，随机性检验 |
绪论
随机数生成器(Random Number Generator,以下简称RNG)是使用计算机软件或硬件生成随机数的装置，这里的随机数特指比特串(bit stream)[1]。 RNG可分为两类：伪随机数生成器(Psuedo Random Number Generator,PRNG)和真随机数生成器(True Random Number Generator,TRNG)，前者使用软件和确定过程计算，而后者至少依赖一种物理上的随机现象。 RNG有3类重要的应用:蒙特卡罗实验[2]、博彩行业和计算机密码学，在这3类应用中，对随机数生成器的要求不尽相同。为此我们需要一些统计学的方法来检验RNG的好坏。
需要注意的是，在不同的上下文，RNG的意义不尽相同。有的文献会把RNG直接指代PRNG，有的会直接指代TRNG，本文中的RNG，总是PRNG和TRNG的超集。
从统计学本身的意义上，RNG又可以分为均匀分布的RNG和某种特定分布的RNG。前者一般生成[0,1]均匀分布的随机数(注意：这里需要将比特串理解为某种长度单元的字串 word stream，每个字表示一个0到1之间的小数)，而后者可以通过前者和相关分布的累计分布函数的反函数求得。因此我们只需关注前者即可。
本文将结合随机数生成器的研究现状，对现有的随机数生成器的本身、使用环境和检验方法做一个综述。本文将按照以下方式组织，第2节讨论RNG的使用环境及需求，第3节介绍几个现有的RNG并讨论其特点，第4节介绍RNG的测试方法，第5节总结。
使用环境及需求
蒙特卡罗实验要求RNG的均匀性要好，而一般不要求其不可预测性，另外，由于对随机数的需求很大(越大结果越准确)，因此也对产生的速度有一定的要求。一般来说，蒙特卡罗实验使用廉价的PRNG就足够了。
博彩行业则要求RNG的均匀性和不可预测性，是TRNG的重要应用场合。
在计算机密码学中，不同的情况对RNG的要求也不尽相同。例如，如果要生成一个RSA密钥对，则需要TRNG，以便生成一个世界上独一无二的密钥对； 如果要做一个类似OTP的流密钥，则要求一个难于破解的PRNG，以便通信双方都能独立生成密钥而第三方在没有种子的情况下无法破解。
从上我们可以总结出RNG的不同需求：
1是均匀性，即严格遵守均匀分布(变换后遵守目标分布)。
2是不可预测性或者随机性，即每个bit或者说每个word都是独立生成的，后生成的bit与前面的bit无关。一个理想的随机数生成器是不断的掷一个公平的硬币，如果掷出正面输出比特1，掷出反面输出比特0[3]。但这个理想的RNG显然是太慢了。
3是生成速度，即每秒输出多少bit。
现有的随机数生成器
这一节分别介绍PRNG和TRNG。
PRNG
最简单的PRNG是线性同余生成器(Linear Congruential Generator, LCG)[4]。 关于LCG，需要仔细选择参数以保证好的随机性[5]。
另外一种常见的PRNG是线性反馈移位寄存器(Linear Feedback Shift Register, LSFR)[6]。
Bob Jenkins发明了一个高效的PRNG:ISAAC[7], 可以应用于流密钥。他甚至给出了一个生成结果(实际上是两个)，悬赏能够破解其内部状态的人。
TRNG
所有的TRNG都与某种物理现象相关。上文提到的掷硬币的理想RNG，就是一种TRNG，尽管这个TRNG因为慢而不实用，但它可是所有PRNG和TRNG的检验标尺。
John S. Denker 利用计算机的声卡采集到的环境噪声，设计了turbid[8]。
Ali Sadr, Mostafa Zolfaghari-Nejad 利用了每个开关单元的延迟特性不一样和LFSR的优点，设计了基于物理上不可复制(Physical Unclonable Function)的高效廉价TRNG[9]。
目前研究的热点，是基于物理学中的量子随机性的TRNG。例如，T. Symul, S. M. Assad等人利用量子光束的功率波动创造了一个高速(高达5.7Gbit/s)的TRNG[10]。他们甚至创建了一个Web服务，可以让人免费安全的下载当前正在生成的随机数串，并且，不同的客户端是不会重复的。
测试方法
RNG的好坏与否，需要通过统计学中的假设检验来测试。目前最常用的测试方法(也是公认的好的测试方法)是美国国家标准与技术委员会(NIST)发布的测试集[3]，包含15个测试。
这15个测试，观察值是某种被试的RNG生成的比特串，模型1如下：
- 原假设H0：该RNG是理想的掷硬币RNG，或者说无法区分该RNG与理想的掷硬币RNG。
- 备择假设H1: 该RNG不是理想的掷硬币RNG。
根据原假设H0可以导出观察值的某种统计学特征(分布模型)，通过该模型计算可计算出一个P值(P-value)，与显著性水平比较，若前者小，则拒绝原假设，否则接受原假设。这里的P值是“尾概率”，表示H0成立时，概率密度与观察值相等或者更小的概率之和(积分)。
以上仅仅描述了一次基本测试。对同一个测试，往往要做n(n>=100)次基本测试，把所有的P值记录下来，然后再做一次如下的假设检验(模型2):
- 原假设H0: P值服从[0-1]均匀分布
- 备择假设H1：P值不服从[0-1]均匀分布
因此，对于好的随机数生成器，做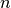 
次基本测试，其拒绝次数与期望次数 
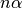接近，其中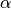 
为基本测试中的显著性水平。
RNG要过NIST的15个测试，每个测试的过程还很长，有没有更简单并且更有效的方法呢？一些人在研究这个问题。B. Ya. Ryabko 和 V.A. Monarev 提出了基于信息论的RNG测试方法[11]，文中给出了两种测试方法，分别称为书栈(Book Stack)法和频序(Order)法。与给出的方法相比较，作者同时指出，无损压缩方法也可以很好的检验随机数。并且无损压缩方法很容易理解： 如果某种无损压缩算法真的把RNG生成的字节串压缩了，则拒绝原假设(模型1)，否则接受原假设。作者同时给出证明，在一定的条件下，无损压缩方法的第二类错误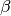 
随着观察值长度的增加趋向于0。利用这两种方法、无损压缩法以及NIST的那15种方法分别对：有缺陷的PRNG(RANDU)生成的字节串、以及公认的好的随机串[12]进行检验，作者给出了一个实验结果，在长度为 
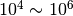bit的观察值条件下，书栈法和频序法的第二类错误 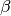明显小于NIST的各种方法。而在 
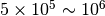bit观察值条件下，NIST的各种方法甚至不如无损压缩算法RAR和ARJ(第二类错误)。直到 
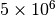bit观察值的条件下，NIST中的离散余弦变换测试方法才勉强能和书栈法、频序法相比，其他的测试要么第二类错误太高，要么第一类错误太高。结果确实很有意思，但是否正确值得使用独立实验验证。
结论
本文介绍了RNG的使用环境及要求，现有的RNG以及RNG的测试方法，作为作者学习RNG的一个笔记，并且希望它能够作为RNG初学者或想进人RNG研究领域人员的一个入门参考。
参考文献
[1] http://en.wikipedia.org/wiki/Random_number_generation [EB/OL]. 2012.
[2] http://en.wikipedia.org/wiki/Monte_Carlo_method [EB/OL]. 2012.
[3] Andrew Rukhin等. A Statistical Test Suite for Random Number Generators for Cryptographic Application[S]. NIST Special Publication 800-22 Rev 1a. 2010.
[4] http://en.wikipedia.org/wiki/Linear_congruential_generator [EB/OL]. 2012
[5] Donald E. Knuth. The Art of Computer Programming[M]. Volume 2, Seminumerical Algorithm. 1997.
[6] http://en.wikipedia.org/wiki/Linear_feedback_shift_register [EB/OL]. 2012.
[7] Bob Jenkins. ISAAC: a fast cryptographic random number generator[EB/OL]. http://www.burtleburtle.net/bob/rand/isaacafa.html . 2012.
[8] John S. Denker. High-Entropy Symbol Generator[EB/OL]. http://www.av8n.com/turbid/ . 2012.
[9] Ali Sadr, Mostafa Zolfaghari-Nejad. Physical Unclonable Function (PUF) Based Random Number Generator[J]. ACJJ， Vol 3, No.2, March 2012.
[10] T. Symul, S. M. Assad, and P. K. Lam. Real time demonstration of high bitrate quantum random number generation with coherent laser light[J]. Appl. Phys. Lett. 98, 231103. 2011.
[11] B. Ya. Ryabko and V.A. Monarev . Using Information Theory Approach to Randomness Testing[EB/OL]. http://arxiv.org/abs/cs/0504006. 2012.
[12] George Marsaglia. The Marsaglia Random Number CDROM including the Diehard Battery of Tests of Randomness[EB/OL]. http://stat.fsu.edu/pub/diehard/. 2012.